１章 検定の論理（二項検定を教材として）
例題1：B薬はA薬より有効か？
本章で取り組む例題を紹介します。とある疾患に対し、従来から定評のあるA薬があるとします。A薬の有効率は0.6です。
有効率は、患者が服用して効果がある確率です。つまり「有効率が0.6」は、無数の患者がA薬を服用した場合に「60%の患者に効果があり、40%の患者に効果がない」を意味します。
さて、A薬より効果の高い新薬を求めて、B薬が開発されたとします。B薬の有効率は、現時点では不明です。
そこで臨床試験を行います。 20人の患者の協力を得たとします。B薬を服用してもらい、効果の有無を観察します。「B薬はA薬よりも有効なのか？」これが知りたい疑問です。
以下、2つのケースを考えます。
1例題1.1：18人に効果がある場合
B薬を服用した20人の患者のうち、18人に効果があったとします。
この場合、20人中18人に効果があったので
と計算して、90%の患者に効果があったことになります。
この0.9という数値は、A薬の有効率0.6より高い数値です。しかし、たった20人の結果から得た数値です。被験者の数が少ないので「この結果から、明確な結論が得られるのか？」という不安が残ります。「一体、この結果から、B薬はA薬より優れていると判断できるだろうか？」という問題を考えます。
2例題1.2：14人に効果がある場合
2つめのケースです。B薬を服用した20人のうち、14人に効果があったとします。
この場合、20人中14人に効果があったので
と計算して、70%の患者に効果があったことになります。
この0.7という数値も、A薬の有効率0.6より高い数値です。しかし、たった20人の結果から得た数値です。被験者の数が少ないので「この結果から、明確な結論が得られるのか？」という不安が残ります。「一体、この結果から、B薬はA薬より優れていると判断できるだろうか？」という問題を考えます。
3例題の解答
結論から書きます。二項検定（binomial test）を使うと、例題1.1では「おそらく、B薬はA薬より優れているだろう」と判断します。一方、例題1.2では「B薬とA薬の間に、差があるのかどうか、分からなかった…」と判断します。
本章では、こうした判断を下すに至った論理の枠組みを学びます。この論理は、全ての検定に共通する、統計学特有の論理です。
二項検定を理解するには、その前に、2つの学習項目、二項分布と期待値を学ぶ必要があります。
二項分布
二項検定の理解には、二項分布（binomial distribution）と呼ばれる確率分布の理解が欠かせません。確率分布（probability distribution）とは、起こりうる全ての結果に対し、その確率が逐一計算された一覧のことです。
二項分布を理解するには、まず、二項係数（binomial coefficient）の復習が必要です。二項係数は、第2章のWMW検定でも、欠かせない予備知識となります。
1二項係数 nCx
私たちは、二項係数を、高校1年の時に組み合わせ（combination）として、すでに学んでいます。
具体例を使って復習します。 緑の玉が2つあるとします。2つの緑玉は、互いに区別がつかないとします。
紫の玉が3つあるとします。3つの紫玉も、互いに区別がつかないとします。
ここで、2つの緑玉と3つの紫玉を、一列に並べてみます。このとき「何通りの並べ方があるだろうか？」という問題を考えます。
この場合、玉の数の合計がたった5個ですから、試行錯誤して、可能な並べ方の全てを揃えることは難しくありません。実際に行うと、以下の10通りの並べ方があることが分かります。
しかし、この方法での数え上げは面倒です。簡単な計算で答えが得られると、助かります。
この答えを教えてくれるのが二項係数nCxです。公式は
です。ここで、nは緑玉と紫玉の数の合計です。xは緑玉の数、もしくは、紫玉の数でもよいです。
今回の例なら、nは
n= 2 + 3 = 5
です。xは、緑玉の数
x = 2
でもよいし、紫玉の数
x = 3
でもよいです。どちらでも、同じ答えを教えてくれます。
実際に計算してみます。すると
もしくは
となります。この計算は10通りという答えを教えてくれます。たしかに、試行錯誤して得た、図と同じ答えになっています。
表記の補足をしておきます。二項係数の表記として、日本では高校で「nCx」と教わります。しかし、国際的には、このCを用いた表記は極めて少数派です。普通は
と表記します。読者がさらに統計学の学習を進めると、この表記が中心となります。そこで、この表記があることを、今の時点で知っておいてください。
2コブ斜面を降りる
二項分布の説明に入ります。二項分布を学ぶ題材は、パチンコかスキーが視覚的で分かりやすいです。本書では、スキーの例で説明します。
ここでは、スキーの初心者がコブ斜面に挑戦することを、単純化して考えてみます。
コブ斜面を、以下のように模式化します。コースの真ん中（三角印）の場所から、斜面を降ります。
この斜面を降りきるために、コブを1つ1つ、左右どちらかによけながら降ります。この例では、5つのコブをよけます。径路の1つを下図に示しました。この場合、ゴール4に降りてきました。
最終的に降りてくるゴールには、ゴール0からゴール5まで、6つの可能性があります。
計算を簡単にしたいので、単純な仮定を立てます。スキー初心者にありがちなように、この初心者は利き足を踏ん張りがちです。そこで、コブを右によけるのと左によけるのとでは、得手不得手があるとします。
今回は、斜面の下から見て、右によける確率を0.6とし、左によける確率を0.4と仮定します。この確率は、常に一定と仮定します。
この仮定の下、以下の6つの確率
● ゴール0に降りてくる確率
● ゴール1に降りてくる確率
● ゴール2に降りてくる確率
● ゴール3に降りてくる確率
● ゴール4に降りてくる確率
● ゴール5に降りてくる確率
を計算します。この全てを計算すれば、二項分布が完成します。
3ゴール2へ降りる確率
本章の内容を冗長にしないために、ここではゴール2へ降りてくる確率だけを、丁寧に見ていきます。
まず、ゴール2へ降りてくる径路のうち、2つを適当に選んで示します。1つめ。
2つめ。
この2つの径路を観察すると、1つの共通点が見つかります。どちらの径路でも、右によける回数が2回で、左によける回数が3回です。試してみると、この「右2回・左3回」以外、ゴール2に降りてくる径路がないことが分かります。
そこで、1つめの径路も2つめの径路も、他の径路も、同じ確率で起こることが分かります。計算は、1つめの径路が
0.6 × 0.6 × 0.4 × 0.4 × 0.4 = 0.02304
で、2つめの径路が
0.4 × 0.6 × 0.4 × 0.6 × 0.4 = 0.02304
です。掛け算の順番が違うだけで、どちらも同じ
0.62 × 0.43 = 0.02304
という式に統一できます。ゴール2に降りる全ての径路が「右によけるのが2回」と「左によけるのが3回」からなる以上、ゴール2に降りる全ての径路が、同じ確率で起こります。
そこで、ゴール2に降りてくる確率は、上記の確率 0.62 × 0.43 = 0.02304 に加えて、ゴール2に降りてくる径路は何通りか？さえ分かれば、計算できます。
ここで二項係数が登場します。節1-21の緑玉と紫玉の並びを再度用意します。緑玉を「右によける」に、紫玉を「左によける」に対応させます。
こう対応させることで、ゴール2に降りてくる径路が、全部で10通りあることが分かります。以下、この10通りの径路を全て並べます。サラッと眺めてみてください。
このように、ゴール2に降りてくる経路が何通りか？を、二項係数が教えてくれます。この図で示したどの経路を通る確率も、全て等しく
0.62 × 0.43 = 0.02304
です。そして、全部で10通りの経路があります。そこで、ゴール2に降りてくる確率は、この2つの積
10 × (0.62 × 0.43) = 0.2304
で得られます。形式を重んじて書き直すと、二項係数を使って
となります。他のゴールに降りてくる確率も、同じ考え方で計算できます。
4二項分布
二項分布の一般式を示します。
コブ斜面の例を使って、記号を説明します。まず、大文字のXです。確率変数（random variable）と呼ばれます。コブ斜面の例なら、Xは、降りてくるゴールの番号です。そして、この大文字のXは「一体、どんな番号のゴールとなるのかは予測できない」という意味を持ちます。次に小文字のxです。xは、降りてくるゴールの具体的な番号で、0, 1, 2, 3, 4, 5です。P(X=x)はゴールxに降りてくる確率です。nは乗り越えるコブの数で、この例なら5です。pはコブを右によける確率で、この例なら0.6です。1−pはコブを左によける確率で、この例なら0.4です。
本書では、二項分布の説明に、スキーを例に使いました。理由は「計算の細部を視覚的に表現できる」です。ただし、一部の学生は、スキーを例にした説明に違和感を感じます。「ゴールにはA, B, C, D, E, Fのように記号を割り当てるのが普通なのに、わざわざ数値を割り当てて、その上で、その数値に数字としての意味を持たせることに違和感を感じる」という指摘を、毎年、数名の学生から受けます。それから、「ゴールの番号を、1からでなく、0から始める理由が分からない」という指摘もあります。
こうした指摘に答えます。本章のスキーの説明では、ゴールの番号、0から5には「コブを右に避ける回数」を対応させています。例えばゴール0は「右によける回数が0回のときに降りてくる場所」です。このような形で、明確に「ゴール0」を「0」という数字と対応させています。ゴール2なら「右によける回数が2回のときに降りてくる場所」です。「ゴール2」の「2」には「2回よける」という形で、数字の「2」に明確に対応させています。ですから、本章のスキーの例では、ゴールの番号には、明確に、数字としての意味があります。
そして、このように定式化しておくと、次節で示すように広範な応用が可能となります。もし、読者が「ゴールの番号」について違和感を感じた場合は、気にせずに、読み進めてください。
こうした値
を二項分布の式に代入すると
となります。この式の右辺を見ると、xだけの関数になってることが分かります。そこで、あとは、xに0, 1, 2, 3, 4, 5を順番に入れていくだけです。これで、ゴールxに降りてくる確率が計算できます。全て計算すると
となります。これで、二項分布と呼ばれる確率分布が完成しました。確率分布は、一覧表よりも、グラフで示すのが一般的です。
二項分布のように、グラフにすると階段状の形状を示す確率分布のことを離散型分布（discrete distribution）と呼びます。
5二項分布の応用
二項分布は、最も基本的な離散型の確率分布です。多くの応用があります。様々な現象の、モデル化や統計解析の基礎となります。簡単な例を3つ紹介します。
❶ コイン投げ
1つめの例は、コイン投げです。
コインを投げることを考えます。表が出る確率がpで、裏が出る確率が1−pであったとします。このコインを5回投げたとき、表がx回出る確率P(X=x)は、コブ斜面と同じ計算で得られます。スキーの図を、次のように読み替えます。
ここで確率pに仮定を設けます。このコインは裏表が非対称で、表が出る確率がp=0.6、裏が出る確率が1−p=0.4だったとします。すると、このコインを5回投げたときに表が出る回数Xの確率分布は、スキーの場合とまったく同じになります。
❷ 街頭調査
2つめの例は、街頭調査です。
街頭で、無作為に選んだ有権者5人に「政府を支持するか？」と質問したとします。真の支持率がpであったとします。不支持の確率は1−pです。このとき、x人の有権者が「支持する」と答える確率P(X=x)の計算では、スキーの図を次のように読み替えます。
ここでpに仮定を設けます。真の支持率がp=0.6であったとします。不支持の確率は1−p=0.4です。すると、無作為に選んだ5人のうち、「政府を支持する」と答える人数Xの確率分布は、スキーの場合とまったく同じになります。
❸ 薬の効果
3つめの例は、本章の例題です。
有効率p=0.6のA薬を、患者5人が服用したとします。効果のある患者の数がx人である確率P(X=x)も、同じ計算で得られます。スキーの図を次のように読み替えます。
有効率が0.6なので、効果がある確率がp=0.6、効果がない確率が1−p=0.4です。そこで、5人の患者のうち、効果がある人数Xの確率分布は、スキーの場合と同じです。
期待値 E[X]
期待値（expected value, expectation）は、確率分布を特徴付ける、重要な数値の1つです。平均とも呼ばれます。その意味は、文字通り「期待される値」です。確率変数Xの期待値をE[X]と書きます。「E」という記号は「expectation（期待値）」の頭文字に由来します。定義は
です。記号を説明します。まず、E[X]の中の大文字Xは確率変数です。スキーの例なら、降りてくるゴールの番号です。小文字xi (x1, x2, x3, ... , xn)は、確率変数Xがとりうる具体的な数値です。スキーの例なら、xiは、0, 1, 2, 3, 4, 5の6個です。piはxiが起こる確率です。スキーの例の場合、piはすでに節1-24で計算しています。
期待値E[X]の計算は「確率piで重み付けした平均」と言えます。以下に、期待値E[X]の計算をスキーの例を使って示します。まず、xiとpiの一覧を用意します。
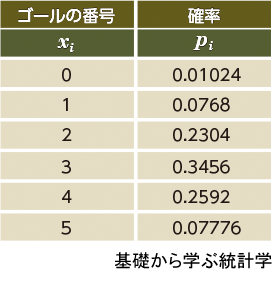
本節の計算例ではxiに「ゴールの番号」を使っています。一部の読者は「これでは実感を伴わない」と感じるかもしれません。その場合は「ゴールの番号」を、前節の応用例「コイン投げで表が出る回数」や「街頭調査での政府支持の人数」「A薬で効果のあった患者の数」で読み替えてみてください。
次に、xiとpiを掛け算します。
最後に、xiとpiの積を合計すれば、期待値E[X]が得られます。
「確率piで重み付けした平均」を補足します。「重み付けした平均」は正確には加重平均と言います。加重平均を説明します。計算に用いる観測値を
x1, x2, x3, … , xn
とします。次いで、それぞれの重みの係数を
w1, w2, w3, …, wn
とします。すると、加重平均は
と計算されます。もし、すべての重みが等しいときは、重みの係数は「全て1」と書けます。
1 = w1 = w2 = w3 = … = wn
このとき、加重平均は
となって、単純な算術平均となります。次に、重みの係数を、確率piにしてみます。加重平均は
です。ここで、1からnまでの、すべての確率piを合計すると1になります。
p1 + p2 + p3 + … + pn = 1
そこで、確率piで重み付けした加重平均は
p1 x1 + p2 x2 + p3 x3 + … + pn xn
となって、期待値の定義そのものとなります。
二項分布における、期待値E[X]の位置を、図で示します。
二項分布の場合、期待値E[X]は、確率が最も高い、確率分布の頂点の位置を教えてくれます。
このAdviceは、読み飛ばしても構いません。上の文章では、厳密には正しくない記述をしています。二項分布の頂点の位置は、以下のように定まります。まず
(n + 1)p
という計算をします。スキーの例なら
(5 + 1) × 0.6 = 3.6
です。もしこの値が整数でない場合、二項分布の頂点の位置は(n + 1)p以下の最大の整数です。スキーの例なら3.6で、整数ではありません。そこで、頂点の位置は3.6以下の最大の整数、3になります。一方、(n + 1)pが整数のときは、二項分布の頂点の位置は、隣り合う(n + 1)pと(n + 1)p－1の2つになります。ただし、こうした知識は、私たちのような統計学のユーザーにとっては、必要ではありません。「二項分布では、期待値E[X]のすぐ側に、分布の頂点がある」程度に理解しておけば、十分です。
練習問題 A
コイン投げを考える。表が出る確率と裏が出る確率は等しく、ともに1/2だと仮定する。
このコインを6回投げ「表が何回出るか？」を考える。結果を事前に正確に予想することは不可能である。しかし、直感的に
6 × 0.5 = 3
と計算して「おそらく表は3回くらいだろう」と予想できる。
この予想「表が3回」が6回のコイン投げの期待値と一致するかをこの練習問題で確認する。6回のコイン投げに対する二項分布は、二項分布の式
に
n = 6 （コインを投げる回数）
p = 0.5（表が出る確率）
を代入して
となる。xに0, 1, 2, 3, 4, 5, 6を順番に代入すれば、以下の確率分布が得られる。
- 問
- この結果を使い、コインを6回投げたときの表が出る回数の期待値E[X]を計算しなさい。そして、下の図で、期待値E[X]の位置を、蛍光ペン等で示しなさい。
この練習問題を行うと、二項分布の期待値E[X]は
E[X] = np
で与えられるだろうと、誰もが感じます。この直感は正しいです。
二項検定
以上で、二項検定を理解する準備が整いました。本章は、ここからが本番です。
以下、例題1.1と例題1.2を使って、二項検定を説明します。二項検定は、全部で5つのステップからなります。この5つは、全ての検定に共通する手順です。
1STEP 1： 帰無仮説H0と対立仮説HA
最初のステップです。帰無仮説（null hypothesis）と対立仮説（alternative hypothesis）という、2つの仮説を立てます。
帰無仮説は記号でH0と書きます。帰無仮説H0は簡単です。基本は「比べるもの同士が等しい」です。例題1なら「A薬とB薬の有効率は、等しく0.6である」という仮説を立てます。
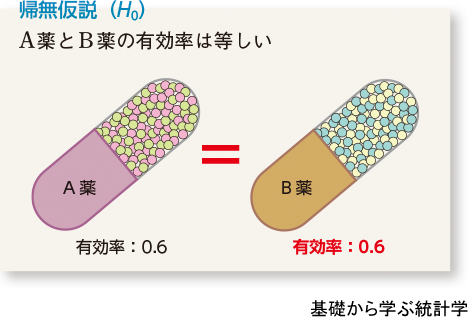
対立仮説は記号にHAやH1を使います。対立仮説HAも簡単です。対立仮説HAは、帰無仮説H0と正反対の内容（もしくは否定の内容）です。「比べるものが等しくない」という仮説を立てます。例題1なら「B薬の有効率は0.6ではない」です。
検定では「帰無仮説H0と対立仮説HAは、実験や調査で得た結果の説明として、どちらが妥当な判断か？」という問題を考えます。
2つの仮説のうち、より重要なのは、帰無仮説H0です。検定は5つのステップからなりますが、大きく分けると、2つの作業からなります。
帰無仮説H0は、検定の根幹をなす概念です。全ての検定は、帰無仮説H0「比べるもの同士が等しい」が正しいと仮定したときに「実験や調査で得た結果は、起こりやすい結果だったか？それとも起こりにくい結果だったか？」を調べます。
2STEP 2：検定統計量
2番目のステップです。実験や調査で得た結果を使って、検定統計量（test statistic）と呼ばれる数値を計算します。
検定統計量は、検定において、最重要の役割を果たします。差があるのか？ それとも、差はないのか？という疑問に対し、最終的な判断を下すための数値です。
一般に、検定統計量の計算は面倒です。しかし、二項検定だけは例外です。何の計算も必要としません。例題1なら、20人中B薬の効果があった人数 x が、そのまま検定統計量になります。例題1.1なら18です。例題1.2なら14です。
3STEP 3：帰無分布
3番目のステップです。帰無分布（null distribution）を作ります。これは、帰無仮説H0「比べるもの同士が等しい」が正しいと仮定したときに、検定統計量 が従う確率分布です。
二項検定は、この点でも易しいです。節1-2の計算法をそのまま使えます。まず、二項分布の一般式を用意します。
P(X=x) = nCx・px・(1−p)n−x
次に数値を代入します。例題1の場合、20人の患者がB薬を服用します。そこでnは患者の数の20です。
n = 20
帰無仮説H0「比べるもの同士が等しい」が正しいなら、B薬の有効率は、A薬と等しく0.6なので
p = 0.6
となります。この2つを代入すると、二項分布の式は
P(X−x) − 20Cx × 0.6x × 0.420−x
となります。ここでxは、B薬で効果のある人数です。
この式で、xを0から20まで、順番に代入していくと、帰無分布が完成します。
要点をまとめます。患者20人のうち、B薬で効果がある人数は、もし帰無仮説H0「比べるもの同士が等しい」が正しいなら、この帰無分布に従います。
4二項分布の特徴
次のステップに進む前に、この確率分布の特徴を観察しておきます。大切な特徴が3つあります。
❶ 期待値E[X]
節1-3の計算に従い、この帰無分布の期待値E[X]を計算すると
E[X]=12
となります。この期待値E[X]=12の意味は「B薬の有効率が0.6であるなら、20人中、その60%の12人に効果があると期待される」です。
帰無分布の中での期待値E[X]=12の位置は
です。12人という結果が出る確率は約18%です。この確率分布の中で、最も高い確率です。
しかし、たったの18%でもあります。これは、5回に1回程度の頻度でしか起こらないことを意味します。そこで「実験や調査の結果が、正確に期待値E[X]に等しくなることは、あまり起こらない」と言えます。
❷ 期待値E[X]周辺の値
次に、期待値E[X]の12人の周囲にある数値を見てみます。ここでは、8人から11人、13人から16人を見てみます。
1つ1つの確率は、期待値E[X]の12人の確率よりも低いです。しかし、全て合計して、期待値E[X]周辺の結果が起こる確率を求めると、約78%です。これは5回中4回程度の頻度です。
そこで「期待値E[X]そのものではなく、期待値E[X]周辺のどれか1つの結果が出る確率が最も高い」と言えます。
❸ 期待値E[X]から、かなり離れた値
最後に、期待値E[X]の12人から離れた値を見てみます。ここでは、7人以下や17人以上を見てみます。
明らかに、こうした結果が出る確率は低いです。7人以下もしくは17人以上となる確率を全て足し合わせても、約4%しかありません。この確率は、とても低いです。
ただし、決してゼロではないことに注意する必要があります。この場合、25回中1回程度の頻度です。ゼロではない以上「絶対に起こらない」とは断言できず、無視はできません。そこで「期待値E[X]からかけ離れた値は、たまに偶然起こりうる。無視はできない」と言えます。
5STEP 4：棄却域と有意水準
本題の、二項検定の手順に戻ります。4番目のステップです。帰無分布に棄却域（rejection region, critical region）と呼ばれる領域を作ります。例題1であれば、7人以下と17人以上の領域を棄却域とします。
棄却域を設定する基本ルールは2つあります。1つめのルールは「棄却域は、帰無仮説H0『比べるもの同士が等しい』の予想から離れた、帰無分布の端っこに設定する」です。例題1の場合、期待値E[X]が12人です。そこで、12人と比べて、多過ぎる人数と少な過ぎる人数の2カ所に棄却域を作ります。このように、帰無分布の両側に棄却域を作る方法を両側検定（two-tailed test, two-sided test）と呼びます。
2つめのルールは「棄却域の確率の合計を5%か1%に設定する」です。棄却域の確率の合計を有意水準（significance level）と呼びます。有意水準の記号にはaを使います。慣習的に、有意水準は、5% (a=0.05) か1%
(a=0.01) に設定されます。実際の統計解析では、5%を採用する場合が大半です。そこで、本書でも「5%」を使うことにします。今回の二項検定の場合なら、左右に2.5%ずつの棄却域を作り、合計5%とします。
ただし、本章の二項検定や、次章のWMW検定の場合、問題があります。確率分布が離散型なので、正確に5%ピッタリになる棄却域が設定できません。この場合、左右の棄却域が2.5%未満の最大値となるように、キリのよい区切りを探し、棄却域を作ります。
6STEP 5：有意差の有無の判断
5番目の、最後のステップです。検定統計量である「B薬で効果のあった患者の人数」が棄却域に入るかどうか、チェックします。
例題1.1では、18人に効果がありました。18は、棄却域に入っています。
この場合、2つの可能性があります。1つの見方は
です。もう1つの見方は
です。
統計学では、検定統計量が棄却域に入ったとき、後者の立場をとります。そこで、帰無仮説H0「比べるもの同士は等しい」を棄却（reject）します。そして「おそらく、対立仮説HA『比べるもの同士は異なる』の方が適切であろう」と判断します。
検定統計量が棄却域に入った場合、レポートや論文では「A薬とB薬の有効率に統計的に有意な差が認められた(P<0.05)」と記述します。「統計的に有意な差」は「有意差」と短く表現されることも多いです。「統計的に有意な（statistically significant）」という表現は「差があるとした判断は、統計学の立場からは、おそらく妥当だろう」という程度の意味の形容詞です。「有意」という用語は「意味が有る」に由来します。文末にある(P<0.05)という不等式は「有意水準5%の検定で認められた有意差である」ことを示しています。
「統計的に有意な差が認められた(P<0.05)」という表現の、正確な意味は、第3章と第9章で解説します。今の時点では、上述した程度に受け止めてもらえたら、十分です。
なお、この例題1.1では、結果の記述において、さらに一歩進めた表現を使うことを薦めます。この例題では、A薬とB薬の2つを比べています。「差があるだろう」と判断した以上、A薬とB薬の有効率は「どちらかが上で、どちらかが下」です。この例題では、検定統計量は18です。18は、帰無仮説H0が予想する期待値のE[X]=12より高く、右側の棄却域に入ります。そこで「B薬の有効率はA薬の有効率より統計的に有意に高かった(P<0.05)」と書くのが適切な結論です。「高かった」と書くことで、実験の結果が、より明確に示されます。
次に、例題1.2です。例題1.2では14人に効果がありました。14は、棄却域に入りません。
帰無仮説H0「比べるもの同士は等しい」が正しいときに起こりやすい、95%の領域に入っています。
この場合「帰無仮説H0『比べるもの同士は等しい』が正しいと仮定しても、実験や調査の結果を十分に説明できる」と判断します。A薬とB薬の間に差があることを積極的に支持する根拠がありません。そこで「A薬とB薬の有効率に統計的に有意な差は認められなかった」と結論します。
例題1.2の場合、帰無仮説H0「比べるもの同士は等しい」がデータを十分に説明しました。そこで「帰無仮説H0は正しく、A薬とB薬の有効率は等しかった」と結論したくなるかもしれません。しかし、この判断は間違いです。あくまで「明確な差を見出せなかった」という表現に止めます。この理由は、第3章で解説します。
検定の論理 （まとめ）
最後に、全ての検定に共通する「論理の構造」をまとめます。
検定の論理は、初学者には「回りくどい」という印象を与えます。しっかり時間をかけて、この論理に慣れてください。慣れてしまえば、簡単です。
練習問題 B
人間には利き腕があるが、これと同様に、人間には利き耳がある。
