両側検定および片側（上側あるいは下側）検定は6-4ですでに説明している．これまで2群の実験で，ある項目を測定するとき，帰無仮説として母平均\(μ_{1}\)と\(μ_{2}\)は差がない，すなわち，\(μ_{1}＝μ_{2}\)とした．\(μ_{1}\)と\(μ_{2}\)はどちらが大きな値になるかは，通常はわからない．そこで，対立仮説は\(μ_{1}≠μ_{2}\)すなわち\(μ_{1}−μ_{2}≠0\)とした．標本データの標本平均\(\bar{X}_{1}\)と\(\bar{X}_{2}\)で考えると，\(\bar{X}_{1}−\bar{X}_{2}\)はプラスになるかマイナスになるかわからない．したがって，\(t\)分布の両端の2.5％ずつの範囲に入れば，有意水準5％で有意差ありとした．このような検定を両側検定とよぶ（図6-11）．未知の影響を調べる場合は，両側検定とすべきである．

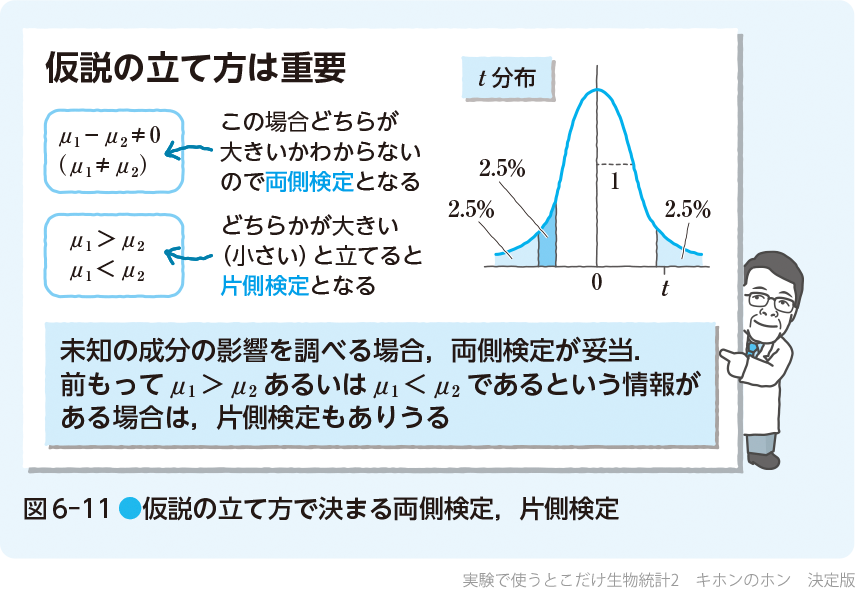
しかし，前もってどちらかが大きいという十分な情報がある場合は，\(μ_{1}＞μ_{2}\)あるいは\(μ_{1}＜μ_{2}\)と対立仮説を立てることも可能である．もし，\(μ_{1}＜μ_{2}\)と対立仮説を立てることができれば，標本データ\(\bar{X}_{1}−\bar{X}_{2}\)はマイナスとなることが最初から期待できることから，図6-11の\(t\)分布グラフのマイナス側だけを考えればよいので，マイナス側に5％を設定できる．このような検定を片側検定とよぶ（この例では下側検定ともよべる．もし，プラス側で5％であれば上側検定とよぶ）．

片側検定では，両側検定よりも\(t\)分布の有意水準の面積が2倍となるので，両側検定よりも有意差が得られやすくなることがわかる（図6-11）．片側検定を使えるのは十分な証明のある場合である（➡6-4）．未知の成分の影響を調べる試験などでは，\(\bar{X}_{1}−\bar{X}_{2}\)はプラスになるかマイナスになるかわからないので，片側検定を用いることはない．

6-4では，「両側」「片側」「上側」「下側」の単語が使われる理由は記述しなかったが，ここを読めばその意味がおわかりいただけたと思う．