第9章 2群間のカテゴリ変数の比較検定 〜カイ二乗検定,Fisherの正確確率検定
2カイ二乗検定,Fisherの正確確率検定とは?
1)検定の概要
ここではカイ二乗検定と
カイ二乗検定では,まず集計された結果から作成されたクロス集計表をもとに,理論上の期待値からなるクロス集計表を作ります.糖尿病の有無と性別の例では実際に集計されたクロス集計表が表9-2であり,その理論上の偏りのない表が表9-1です.そして,偏りのない理論上のクロス集計表と実際のクロス集計表を比べて偏りを検定します.具体的には,その2つの表から検定統計量(カイ二乗値)を算出し,その値とサンプル数からP値の概算をします.


一方,Fisherの正確確率検定は,集計数の中の1番少ない数の群において,その発生数以下になる事象が起きる確率を計算した値がP値になります.表9-4の場合は,一番少ない数は39(治療なし,男性のマス)なので,「治療なし,男性」が0〜39となる場合(40通り)のそれぞれの確率を求めて足し合わせた値がP値です.そのため,少なくとも40回の計算が必要です.表9-3の場合は,最小値が191(治療なし,男性のマス)なので,192回の計算が必要になります.コンピューターの性能が上がった現在では,あまり計算時間がかからないかもしれませんが,昔はFisherの正確確率検定を行うのは現実的ではなく,カイ二乗値の推定でP値の近似値が得られるため,カイ二乗検定が行われていました.


2つの方法の違いは,計算方法だけです.検定している対象は同じであり,カイ二乗検定は,近似したP値を,Fisherの正確確率検定は直接計算したP値を算出します.
2)カイ二乗検定とFisherの正確確率検定の使い分け
カイ二乗検定,Fisherの正確確率検定と2つの検定を説明していますが,どのように使い分けるべきでしょうか.基本的には,ほぼ同じ値になります.サンプル数の少ない研究では,カイ二乗検定とFisherの正確確率検定との誤差が大きいことがわかっており,一般的に2×2表のときに,症例数が20例以下の場合,または症例数が40以下であっても各セルの期待値(期待度数)が5以下のマスが存在するときはカイ二乗検定ではなくFisherの正確検定を使うとよいとされていますが,すべてカイ二乗検定で問題ないという主張もあります(コラム4参照).いまだに必ずどちらを使うべきという統一されたルールはありません.
課題
12新規治療Xと標準治療の男女の割合の差を検定する
 コマンド入力
コマンド入力

表9-5のようなクロス集計表+P値の表を作成するのが目標です.今回は,カイ二乗検定を行いましょう.Fisherの正確確率検定や使い分けのときに基準にする期待値はコラム5を参照してください.
Stataではカイ二乗検定・Fisherの正確確率検定を同時に行うことができます.クロス集計表を作り,検定をするときはコマンド「tabulate」を使用します.構文は,
tabulate⬚アウトカム変数⬚曝露変数,⬚chi2⬚column
構文において,アウトカム変数(比べたい変数)と曝露変数(比較する群)を入れ替えても,同じ結果が算出されます.「,」の後に続く,chi2はカイ二乗検定,また,columnは列ごとに割合を算出することを指定しています.ちなみに,「row」をつけると,行ごとに割合を算出し,「exact」をつけるとFisherの正確確率検定を行うことができます.
では,サンプルデータにおけるコマンドを入力してみましょう.性別のアウトカム変数は「male」,新規治療X群の曝露変数は「trentment X」です.コマンド入力のルールは第5章で確認しましょう.
tabulate⬚male⬚treatmentx,⬚chi2⬚column
 クリック操作
クリック操作

❶メニューバーから「統計」→「要約/表/検定」→「度数分布表」→「二元配置表/関連係数」を選択.

❷メインタブの「行の変数」は“male”を選択→「列の変数」は“treatmentx”を選択.
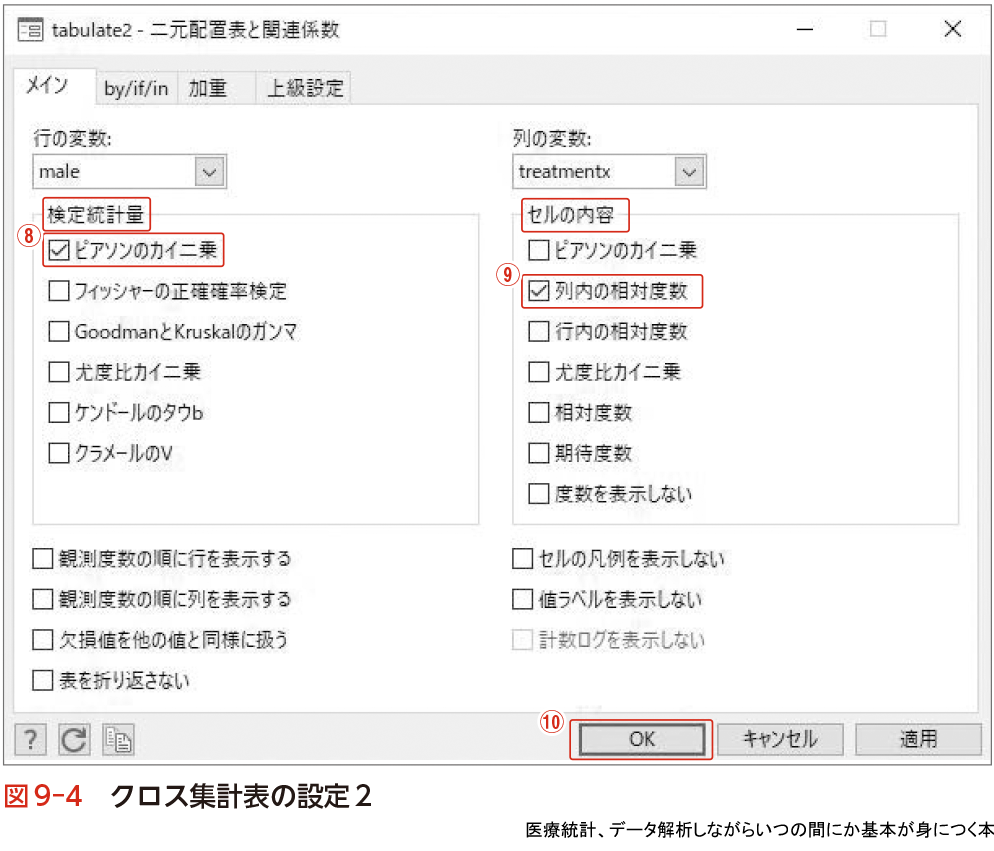
❸メインタブの「検定統計量」は“ピアソンのカイ二乗”,「セルの内容」は“列内の相対度数”をチェック.
❹最後に“OK”をクリック.
 結果の解釈
結果の解釈

結果は図9-5のようになります.さまざまな値が出力されますが,左上のKeyと書かれている四角い枠のなかに,クロス集計表の各欄に出力されている値の内容が表示されます.本表の各欄の数値では上からfrequency(度数,人数),column percentage(列の割合)をあらわしていることがわかります.表の下にある「Pearson chi2(1)=」が検定統計量(カイ二乗値),「Pr=」がカイ二乗検定のP値です.
したがって,この結果は,全体の人数は1,000人で,新規治療Xなし群の女性は266人(58%),男性は191人(42%),新規治療Xあり群の女性は275人(51%),男性は268人(49%)であり,そのカイ二乗検定の結果はP値0.017であると読みとれます.これは「新規治療Xと標準治療の2群間には,男女の割合の差を認める(P=0.02)」と解釈します.
参考文献
- Pearson K:X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 50:157-175, 1900
- 「Mathematical Methods of Statistics Princeton Landmarks in Mathematics」(Cramér H), Princeton University Press, 1946
- Agresti A:A Survey of Exact Inference for Contingency Tables. Statist. Sci., 7:131-153, 1992
- Fisher RA:On the Interpretation of χ2 from Contingency Tables, and the Calculation of P. J R Stat Soc, 85:87-94, 1922
- Lydersen S, et al:Recommended tests for association in 2 x 2 tables. Stat Med, 28:1159-1175, 2009
- Lydersen S, et al:Choice of test for association in small sample unordered r x c tables. Stat Med, 26:4328-4343, 2007
- Martín Andrés A, et al:Comments on “Two-tailed significance tests for 2×2 contingency tables: What is the alternative?”by Robin J Prescott Statistics in Medicine 2019;38:4264-4269. Stat Med, 39:510-513, 2020
- Prescott RJ:Two-tailed significance tests for 2 × 2 contingency tables: What is the alternative? Stat Med, 38:4264-4269, 2019
- 松山 裕:カテゴリカルデータの解析(<連載>統計学再入門 第4回).心身医学,53:874-879,2013
- 「医療統計解析使いこなし実践ガイド 臨床研究で迷わないQ&A」(対馬栄輝/編),羊土社,2020
- 「統計学演習」(村上正康,安田正実/著),培風館,1989
- 「Rによる統計解析の基礎」(中澤 港/著),ピアソン・エデュケーション,2003



