Smart Lab Life

第9回 秘宝：確率分布曼荼羅の発見！

確率分布曼荼羅：生き延びるための地図

前回までの解説で登場した確率分布はベルヌーイ分布，二項分布，正規分布のたった3つだけでした．実はパラメトリック統計学にはほかにもさまざまな確率分布が用いられています．いったいどれくらい多くの確率分布があるのでしょうか．数え方にもよりますが，離散型と連続型を合計すれば，100を大きく上回っていることはまちがいないでしょう1）．読者のみなさんがかつて勉強したかもしれない数理統計学の本にも多くの確率分布が載っていたかもしれません．しかし，私たちが想像するよりもはるかに多くの確率分布が提唱され，それぞれのもつ数学的性質と適用事例が研究されてきました．

たとえば，数年前にアメリカ統計学会誌に発表された 「一変量確率分布の相互関係」2）という論文には全部で76個の確率分布が含まれており，その内訳は連続型57個と離散型19個です．この論文にはこれらの確率分布を一覧できる「チャート」が添付されていることに注目しましょう （図1）．

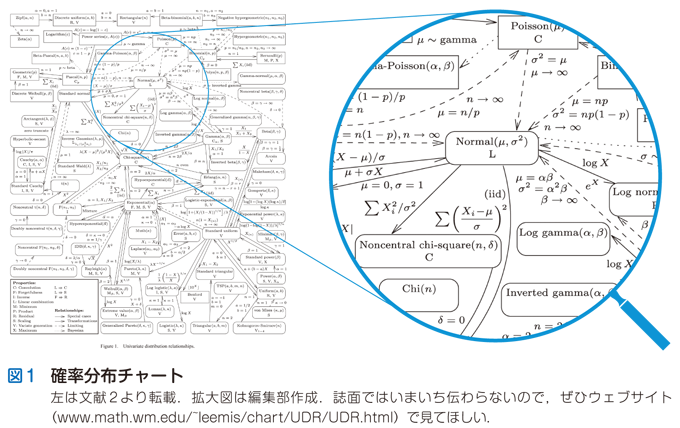
このチャートをはじめて目にしたみなさんは，予想以上の数の確率分布がすでに命名されていることにまず驚かされるでしょう．丸枠は連続型確率分布を意味し，角枠は離散型確率分布を表します．そのなかには正規分布 〔Normal（μ，σ2）〕 や二項分布 〔Binomial（n, p）〕 のような名の通った有名な確率分布もあれば，生物統計学が本職である（はずの）私ですら見たこともないような名前の確率分布さえあります．このチャートはこれらの確率分布すべてを1枚の図によって可視化する試みといえます．

さらに，このチャートに登場する確率分布どうしを結びつける緊密な関連性が見出され（チャート中の矢印），しかもそれらの関連性はすべて数学的に厳密な証明が与えられていることに注目しましょう．数学的に裏付けられたこの基礎があるからこそ，パラメトリック統計学の城は難攻不落なのだと実感せざるを得ません．

このチャートを作図した著者であるLawrence M. Leemis教授はさらにウェブ版のチャートもインターネット公開しています （http://www.math.wm.edu/~leemis/chart/UDR/UDR.html）3）．元論文のチャートにクリッカブルマップとしてのユーザーインターフェースが装備され，ある確率分布にポインターを置くだけで，その確率分布の周囲に配置された関連確率分布が浮かび上がるように設計されています．さらに，ある確率分布をクリックすると，それに関する詳細（関数の数式とパラメーターの説明など）がリンクされていて，とても教育的でしかもおもしろいサイトです．

東洋の思想世界では，世界のかたちを一幅の絵として描き出したものを「曼荼羅（マンダラ）」とよんできました．この確率分布チャートは，パラメトリック統計学の世界をかたちづくる個々の要素（すなわち確率分布）の間の関連性を可視化した「確率分布曼荼羅」と見なすことができるでしょう．

正規分布の帝王学：中心極限定理という神ワザ

確率分布曼荼羅に登場するおびただしい数の確率分布のなかでも，正規分布は特異な地位を占めています．それはかつてラプラスが証明した中心極限定理（central limit theorem） とよばれる強力な定理のおかげです．この中心極限定理によれば，もとの確率分布が何であれ，その母集団から抽出したデータから計算された集計値（総和や標本平均）はサンプルサイズが無限大になると正規分布をすることになります．

中心極限定理がいかに強力であるかを示す一連の図をお見せしましょう （図2）．ここでは4つの確率分布 （Normal＝正規分布，Gamma＝ガンマ分布，Uniform＝一様分布，Beta＝ベータ分布）を用います．各母集団からのサンプル回数は10,000個に設定します．数学的にはもっと厳密な証明が必要になりますが，その定理がどれくらい威力があるかは図2のようなシミュレーションをすればすぐに納得できます．

統計学のサンプリング理論において標本平均はもっとも重要な統計量の一つです．実際，私たちが母集団からサンプルを抽出し，得られたデータから解析をはじめる際に，まずはじめに計算するのは標本平均です．サンプルサイズが増大するにつれ，この標本平均が正規分布に収束すると主張する中心極限定理は，パラメトリック統計学ワールドにおいて正規分布を “無敵” の確率分布に担ぎ上げるのに十分でした．

確率分布曼荼羅はパラメトリック統計学の天守に正規分布をいただく王国を可視化しました．一般の統計ユーザーが確率分布曼荼羅の細部にいたるまで理解するのは，読者のみなさんもおわかりのように，容易なことではありません．しかし，数学的な厳密さの証明は専門の統計学者たちにお任せすればいいのではないでしょうか．むしろ，私たちに必要なのは，そのような統計理論が研究現場でどのように使えるのかを理解することだと私は考えます．次回からは実際のデータに対してこれらの統計理論がどのように適用されるかをみることにしましょう

文献

1. Crooks GE：Survey of Simple, Continuous, Univariate Probability Distributions. Version 0.5., 2013　http://threeplusone.com/Crooks-GUDv5.pdf
2. Leemis LM & McQueston JT：Univariate Distribution Relationships. The American Statistician, 62：45-53, 2008　http://www.math.wm.edu/~leemis/2008amstat.pdf
3. Leemis LM：Univariate Distribution Relationships.　http://www.math.wm.edu/~leemis/chart/UDR/UDR.html