Smart Lab Life

第12回 統計データ解析の地上世界と天空世界 ―連載の総括として

乱塊法―もう一つの実験計画法の例として

前々回と前回（第10回，第11回）に説明した完全無作為化法に基づく実験計画法は，反復実施と無作為化という2つのスローガンを組み込んで実験区を配置します．今回お話しする乱塊法（randomized block design）は，これら2つに加えてさらに局所管理というスローガンを掲げます．

まずは実際の例をお見せしましょう．実験計画法の事例と同じく，この実例もまたフィリピンの国際イネ研究所（IRRI）で実際に行われた農業実験です^1）．この実験は，種もみの播種密度がイネの収量にどのような影響を及ぼすかを調べる目的で実施されました．種もみの播種密度は6水準（ヘクタールあたりの種もみの重量にして25 kg〜150 kgの範囲）で設定し，反復数は4回です．もしもこの実験を完全無作為化法によって実施したならば，圃場をまずはじめに6水準╳4反復＝24実験区に分割し，圃場全域にわたる無作為化配置をすることになったでしょう．

乱塊法とはあらかじめ反復ごとに「ブロック」を分割し，各ブロックの中で6水準すべてを無作為化配置するという実験区の割り付けをする方法です（図1）．実験計画法では無作為化をどのように実施するかによって違いが生じます．完全無作為化法の無作為化は，実験圃場に潜む環境要因がデータにどのような影響を及ぼすかがわからない状況で，そのバイアスを回避するという目的で行われます．一方，乱塊法は，実験に用いる圃場に関して事前に背景要因の傾向性がわかっているという状況で用いられる方法です．たとえば，図2のような場合を考えてみましょう．

実験に使おうとするある圃場に関して，東西方向（図の左右方向）に水条件に関する勾配があり，左側の場所は湿潤であるのに対し，右側は乾燥していることが事前にわかっていたとします．ある作物の収量に関する実験を予定しているならば，水条件の違いは得られるデータに大きな体系的バイアスをもたらすでしょう．このとき，水条件の勾配に“直交”する方向にブロックを切れば，データに影響を及ぼす可能性がある水条件を統制することができます．

図2では3つのブロックを設定し，乱塊法に基づいて6水準の無作為化配置をしました．このとき各ブロックは水条件に応じて左から「湿潤ブロック」「中間ブロック」「乾燥ブロック」と名づけられるでしょう．重要なのは，水条件に対応してブロックを切ることで，各ブロック内の環境条件をそろえた点にあります．これが第三のスローガンである局所管理です．すべての水準は水条件の異なるブロックでそれぞれ実施されるので，水準のもつ効果をよりはっきりと調べることができる．これが乱塊法の長所です．マウス実験の例では，マウスの血統，体重などがブロックごとに均一に配されるように設計することになります．

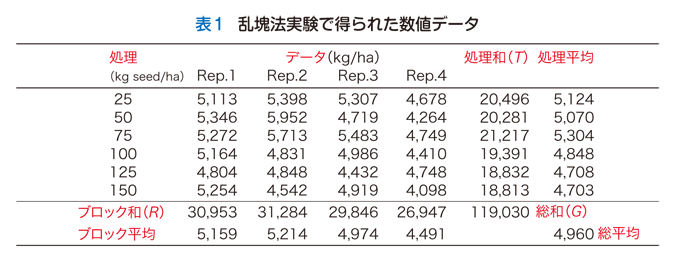
上の図1の乱塊法実験のもとで得られた数値データは表1のようになりました．このデータ表を各水準の行ごとに横方向に集計すれば，完全無作為化法の場合と同じく，処理平均を求めることができます．ところが，乱塊法ではそれに加えて列ごとに縦に集計することにより，ブロック平均も計算できます．処理平均は水準ごとの効果の大小を，そしてブロック平均はブロックごとの効果の大小を数値化しています．乱塊法の線形統計モデルを図3に示します．

そうです．観測データ（x_ij ）が総平均（μ）のまわりでばらつく要因は，右辺に示されているように，処理効果（α_i ）とブロック効果（ρ_j ）そして誤差項（ε_ij ）です．誤差項は水準i と反復 j に関係なく常に同一の正規分布N（0，σ²）に従うと仮定します．完全無作為化法よりも複雑なこの線形統計モデルには，ブロック効果が明示的に含まれていることに注意しましょう．この統計モデルをことばで説明するならば，第 i 水準・第 j ブロックから得られたデータx_ij は，第 i 水準効果（α_i ）と第 j ブロック効果（ρ_j ）の和に加えて誤差項（ε_ij ）を含むということになります．

この統計モデルに基づく偏差の分割は表2に示す通りです．目標はデータのもつ全偏差を処理偏差・ブロック偏差・誤差偏差の3つに分割することです．完全無作為化法で示した手順を適用すれば，続く平方和と平均平方の計算を実行し，最終的に誤差平均平方を分母として処理平均平方を分子とするF値，ならびに同じ誤差平均平方を分母に対してブロック平均平方を分子に置いたF値が計算できます．これらをまとめた分散分析表を表3に示します．この実験ではブロックは有意な効果が見出されました（F＞F_0.01）が，処理に関しては有意な効果は検出できませんでした．

乱塊法の帰無仮説は，完全無作為化法と同じく，処理効果とブロック効果をともに含まない，誤差項のみの統計モデルです．上の分散分析では処理効果とブロック効果を含む対立仮説の統計モデルに対してF検定を実施し，要因が有意であるかどうかをF検定しました．観察データのもとで，どのような統計モデルを当てはめるのが妥当なのかという議論は，モデル選択（model selection）というもっと大きな問題につながっていきます．

総括―情報可視化，統計モデリング，アブダクション

統計学は生きているサイエンスの1つとして，時代の風潮や傾向と無縁ではありません．今風には“データ・サイエンス”と呼ぶ方がカッコイイようですが，いわゆる“データ・ドリヴン（data-driven）”な科学研究は，大量の情報と高性能コンピューターの追い風に乗って，今後さらにその影響力を増していくのかもしれません．その一方で，科学研究の場だけでなく，いま私たちが生きている現代社会のなかでも，より多くのデータや情報を手にすることにより，あたかも宝探しのように“金脈”が掘り当てられるというちょっと都合のいいイメージが膨らんでいるようです．

しかし，本連載ではもっと地道な案内図をみなさんに提示しました．実験や観察を通して私たちが手にするデータには，それを生み出した因果構造がどこかに埋め込まれています．定量化された数値データはそのままでは私たちには解読できません．そこで，さまざまな統計グラフィクスのダイアグラムを利用することで，データの示すふるまいは誰もが理解できるように可視化することができます．万人がわかること―まさにこれが統計的データ解析の原点であるはずです．

エドワード・R・タフティ（Edward R. Tufte）は，長年にわたって，数値データをいかにして“見える”ようにできるかというデータ可視化（data visualization）の問題に取り組んできました^2）．昔から私たち人間は膨大かつ複雑なデータを可視化すべく試行錯誤をくり返してきました．つい最近私が翻訳したマニュエル・リマ（Manuel Lima）の最新刊『THE BOOK OF TREES―系統樹大全』^3）もまた，多様性情報の可視化をめぐる一千年に及ぶ知的系譜を明らかにしてくれました．データや情報を視覚化するインフォグラフィクス（infographics）を単なる流行語のまま終わらせるのではなく，現場で利用できる実質的なツールとして鍛えあげることが必要とされています．統計的データ解析はこの目標を見失ってはなりません．

その一方で，データや情報は既知の知見から未知なるものへの推論，すなわちアブダクションを目指すというもう一つの目標があります．形態測定学者フレッド・L・ブックスタイン （Fred L. Bookstein） の大著^4）に力説されているように，データの統計モデリングを通じて，私たちはよりよい暫定的結論を導くことができます．ただし，このアブダクションという推論には終わりがありません．真実を前提としないアブダクションは，新たなデータが出現するたびに新たなよりよい （しかしやはり暫定的な） 結論へと移行します．

膨張し続けるデータの可視化と，はてしないアブダクションの連鎖―身の丈サイズの統計学は情報の海とモデルの山を越える翼を私たちに与えてくれます．

おあとがよろしいようで．

文献

1. 「Statistical Procedures for Agricultural Research, Second Edition」（Kwanchai A. Gomez & Arturo A. Gomez）, John Wiley & Sons, 1984
2. 「The Visual Display of Quantitative Information, Second Edition」（Edward R. Tufte）, Graphic Press, 2001
3. • 「The Book of Trees: Visualizing Branches of Knowledge」（Manuel Lima）, Princeton Architectural Press, 2014
   • 「THE BOOK OF TREES—系統樹大全：知の世界を可視化するインフォグラフィクス」（マニュエル・リマ／著　三中信宏／訳），ビー・エヌ・エヌ新社，2015
4. 「Measuring and Reasoning: Numerical Inference in the Sciences」（Fred L. Bookstein）, Cambridge University Press, 2014