§ 涙なしの統計学は可能か

講師のひとりとして私も参加したある統計研修の受講生が別の講師が担当した講義内容に関して次のような質問を投げました：

読者のみなさんもご存知のように，いわゆる数理統計学の理論体系では，現実世界のデータの挙動をある数式で表現された確率密度関数をもつ確率分布によってモデル化します．たとえば，確率変数（変量）が連続的ならば正規分布，離散的ならば二項分布のような確率分布がこれまで数多く提示されてきました．そして，数理統計学に基づく統計分析の本道は，いかにすればこれらの確率分布の数学的性質に基いて推定や検定ができるのかを論じることにありました．

１世紀以上も前にカール・ピアソン（Karl Pearson：1857〜1936）が敷いた（当時の言葉で言えば）「生物測定学（biometrics）」の基本路線のうえに，数理統計学は壮大な理論の砦を築き上げ，ロナルド・A・フィッシャー（Ronald A. Fisher：1890〜1962）らそうそうたる生物統計学者たちは農学・遺伝学・進化学など数々の応用分野へのその適用を推し進めてきました（統計学の近代史については文献１参照）．数理統計学は，研究者たちが日々の研究の場で手にする“生のデータ”を一貫して「数理の視点」から分析してきたのです．

しかし，上の質問者が書き綴った悩みは，そのような数理統計学の厳密な手続きの妥当性にあるのではなく，むしろ，そのような「数学」の体系そのものと（おそらく質問者にとって）日常的な仕事とがどのようにかかわるのかが掴みきれない点にあるのだと私は理解しました．

数理統計学の根幹は，置かれた前提から導出される命題群が形づくる演繹的体系です．一方，現実の研究の場で問題になるのは得られた知見（データ）からいかにして妥当な推論を実行するのかという点です．したがって，統計学的データ解析とは，数理統計学の立場からいえば，数学的理論体系をよりどころとする，データに基づく推論ということになるでしょう．この観点をとるかぎり，数理統計学をきちんと学ぶ以外に道はありません．

でも，私は生物統計学の講義の最初に，「数学は統計学的思考にとって必須ではない」と必ず言うことにしています．数理統計学の威力を認めたうえで，なお数学とは別のルーツを統計学的思考が有していると信じているからです．今回はその点について説明することにしましょう．

§ ジョン・テューキーと探索的データ解析

数理統計学の理論は第二次世界大戦をはさんで連綿と発展し続けました．そのかたわらで，戦後の統計学の新たな動きのひとつとして特筆されるべきは，ジョン・W・テューキー（John W. Tukey：1915〜2000）が提唱した探索的データ解析（EDA：exploratory data analysis）でした．統計学を「純粋数学」としてではなく「データ解析」の観点から再検討しようとしたテューキーは，今から半世紀前に書かれた長大な総説論文「データ解析の将来」の冒頭で，自らの考えを次のように表明しました：

長い間，私は自分のことを個々の事例からの一般化に関心をもつ統計学者だとずっと思っていた．しかし，数理統計学の進展を見わたしたとき，自らの信念がぐらつく感を禁じ得ない．（中略）要するに，私の主たる関心は“データ解析”にあるのだ．ここでいうデータ解析とは以下を意味している：データを分析する手順，その手順から得られた結果を解釈する技法，解析をより容易かつ高精度かつ高確度にするデータ収集のプランニング，そしてデータの分析に適用された（数理）統計学の手法と結果のすべてである（文献２，p.1より引用して翻訳）

テューキーの持論は，数学的に厳密な統計理論だけでは十全なデータ解析を遂行するには力不足であるという点にありました：

“数理統計学”のさまざまな成果は，データ解析の実践と結びつかないかぎり，あるいはいつかどこかでそれと結びつこうとする心構えがないかぎり，“純粋”数学とみなすしかなく，それ自身の基準に照らして批判されなければならない．数理統計学の成果はデータ解析かそれとも純粋数学のいずれかに照らして正当化されるべきである．（中略）概して言えば，統計学における大革新はデータ解析における大躍進をもたらさなかった．今こそデータ解析を刷新すべき時ではないか（文献２，p.3より引用して翻訳）

停滞していた当時の「データ解析」を刷新すべく，テューキーが開発した方法が「探索的データ解析」でした．1977年にやっと出版された同名のオレンジ本（文献３）―表紙カバーがオレンジ色なのでそうよばれる―には，全編にわたって彼独自のデータ解析手法が展開されています．とりわけ，探索的データ解析が，後述する「幹葉表示」や「箱ひげ図」のような，斬新な統計グラフィクスを多用した点は特筆されるべきでしょう．数理統計学が数学と計算によるアプローチを目指したとするならば，テューキーはダイアグラムを用いた直感的なアプローチを模索したといえます．

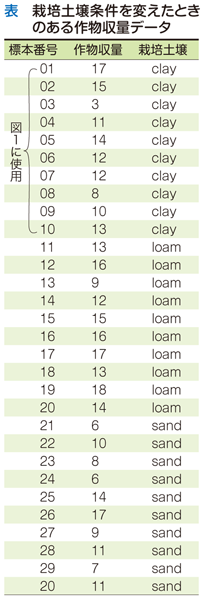
たとえば，次のような実験データ（表） を例に取りましょう：

この実験は，ある作物の収量が３通りの栽培土壌条件（「clay」＝粘土／「loam」＝ローム／「sand」＝砂）によってどのように変わるかを調べるために，それぞれの土壌条件（水準）ごとに10個体ずつ計30 標本に関して得られた収量データです．たとえば，粘土で栽培された10標本を収量（yield） に関する散布図で示すと図１になります．

この図1に示された生データに対して， テューキーの探索的データ解析は，いっさいの統計計算を介在させずに，データのもつ特徴をグラフィクスを用いて浮かび上がらせようとします．彼が開発したひとつの技法が次の図２に示す「枝葉表示（stem-and-leaf display）」です．

枝葉表示を作成する手順は下記のとおりです：

1. 図1の10標本を大小順にソートし，最大値および最小値のそれぞれからメディアン（中位数）に向かって番号を付していく．このデータセットは偶数個のデータを含むので，メディアンはソートした５番目と６番目のデータ値の平均（＝12）として求められる
2. 最大データ値は20に達しないので，すべてのデータの十の位は「０」または「１」となる．この２つの整数値が「幹」を構成する
3. 各標本データはそれぞれ一の位の値を用いて「幹」から発する「葉」として連結的に表示する

枝葉表示は，あるデータセットがもつばらつきの特徴を標識値であるメディアンを基準として簡略化して表現しています．そして，この枝葉表示のもつヴィジュアル性をさらに強調したダイアグラムが，現在でも多用されている「箱ひげ図（box-and-whisker plot）」です．図2の枝葉表示を踏まえた箱ひげ図を図3に示しましょう．

この箱ひげ図ではメディアンを太線で書きます．そして，このメディアンと最小データ値との中位点（下四分位点）ならびにメディアンと最大データ値との中位点（上四分位点）を求め，両四分位点を上辺ならびに下辺とする「箱」を描きます．定義により，この「箱」が示す範囲には全標本の半数が含まれます．次に，「箱」の上下辺から「箱」の範囲の1. 5 倍の長さをもつ線分を記入し，「ひげ」とします．この「ひげ」よりもさらに外側に位置する極端に大きい（または小さい）値をテューキーは「外れ値（outlier）」とみなしました．図3では標本番号「３」のデータが３という極端に小さな値をもっていて，外れ値と判定されました．

このように，元の散布図から枝葉表示，次いで箱ひげ図と段階を踏むことにより，データのもつ挙動あるいは癖を直感的かつヴィジュアルに理解することができます．

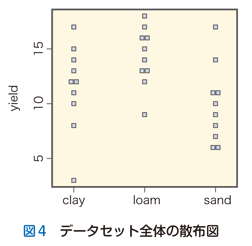
図4 と図5では，30標本すべてを含むデータセットの散布図と箱ひげ図を示しました．

これらの実例を通して，数理統計学の複雑かつ難解な計算をする前にやるべきことがあると主張したテューキーの探索的データ解析の精神の一端をうかがい知ることができるでしょう．

§ 直感的な素朴統計学の強み

さまざまな場で生物統計学を教えてきた私の目から見ると，あまりにも多くの受講生がデータ解析とは統計学であり，その統計学とは数理統計学すなわち（自分たちには理解できない）数学にほかならないという先入観を抱かされてきたようです．生物科学系や農学系の大学教育カリキュラムの大部分では，たとえ「統計学」と銘打たれた講義があったとしても（まったくないこともある），それは数理統計学であることが多く，受講生には必ずしも浸透しているとはいえない状況です．

ここ数年，ある農学系大学の学部生を相手に生物統計学の講義を担当しています．多くの学生は中学から高校の時点で早くも「数学の苦い記憶」を植え付けられ，大学に入ってもそのトラウマを引きずっていることがあります．私はその事情を十分に理解したうえで，毎年の初回講義では，必ず「統計学は数学ではない」「データ解析の第一歩はデータを“見る”ことである」と宣言しています．その上で，テューキーの探索的データ解析が提唱する箱ひげ図などの視覚化技法を実際に見せながら，データを“見る”ことの重要性を学生に刷り込みます．

学生側の反応はきわめて敏感で，次のような感想がいつも届きます：

観察データをしっかり「見る」ことはデータ解析の出発点です．多くの人は，統計分析といえば数式を用いて複雑な「計算」をするものと思い込んでいますが，それは勘違いです．テューキーの探索的データ解析から私たちが学ぶべき教訓は，いっさいの「計算」をする前に，データをちゃんと「見る」そして「読む」心構えを身につける必要があるということです．

文献

1. 『統計学を拓いた異才たち：経験則から科学へ進展した一世紀』（ デイヴィッド・サルツブルグ／著　竹内惠行・熊谷悦生／訳），日本経済新聞出版社，504 pp., 2010
2. Tukey, John W.：The future of data analysis. Ann. Math. Statist., 33：1-67, 1962
3. Tukey, John W.：Exploratory Data Analysis. Addison-Wesley, Reading, xvi ＋ 688 pp., 1977

TOP